How uniform is MD5

If we didn't care about storage and efficiency, this would work just fine. We would also need to consider that our dice is "fair": it returns each face with the same probability. This is, however, not practicall at all: if you wanted to keep the same assignment across multiple runs (which you want if you're running an experiment), you would need to pay the cost of a lookup on an external DB. Keeping the data in memory is not feasible unless your population is really small.

With that in mind, the next obvious question is: can I derive a number from my tuple (user, context) and somehow use that number to "roll the dice"? It turns out there's a whole family of functions that could help us with that: turning data into numbers is what hashing functions are for.

The basic idea of a hashing function is something like this:

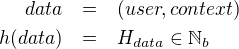1

where 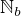is the set of natural numbers that can be represented in 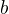bits (that would be the size of the digest). With that generic definition, we will look into three of these hashing functions:

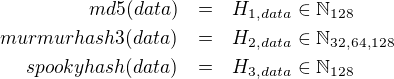2

The hashing value returned by each one of these functions is the same given the same data, but different from each other:

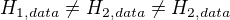3

The difference between MD5 and the other two (MurmurHash3 and SpookyHash) is that MD5 is a cryptographic hash function. Although long time ago MD5 was proven to be weak to be used as a cryptographic function, it's still very popular as a regular hashing function: to prove that data is not corrupted, or, like in our example, to try to correlate some data to a random number.

It is expected from a hashing function to try to be as uniform as possible: this means that given an arbitrary data feed into the function, it should try to return numbers that are spread as much as possible in the output range. As a more concrete example, if your hashing function had a digest of 1 bit (either 0 or 1 are the only two options), then if it's uniform then it should return 0 or 1 with equal probability (it should be a fair coint toss).

With that information at hand, we can now try to prove how uniform are these hashes.

Let's work with our 1 bit hashing function for a little bit. Let's actually give it a name: coinhash.

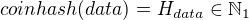4

If we run cointoss 100 times with 100 different data arguments, we would expect it to return 50 times 0 and 50 times 1. If it's too far apart, then we would say it's not uniform for our data set.

What does it mean not too far apart? how can we measure it?

It turns out that there's a statistical test for that, the 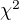test (Chi Squared test). The Chi Square test is used to determine significant difference between two distributions (expected and measured). If you want to learn more about Chi Square, I highly recommend you to look at the videos at Khan Academy on the subject.

For our experiment, running a Chi Squared test will return two important values, the Chi Square statistic, and a probability (p-value) that will tell us how probable is that we would get that statistic (the statistic is basically the normalized squared sum of the difference between the expected and the observed values).

We'll use the following python libraries:

import numpy as np
import mmh3
import struct
import md5
import sys
import numpy as np
import json
import socket
import random
import spooky_hash
from uuid import uuid4
from scipy import stats

We'll create a small dataset that probably will resemble what we'll by trying to do in real life: according to some specific user data (userid + some context), get a unique (hopefully random) number.

For that, we'll generate 5 million random users and store them in a "json-lines" text file, that we'll later use to test all three hashing functions (same dataset for all three).

TOTAL_RECORDS = 5000000
FILENAME= '/home/rolando/Documents/www.rolando.cl/wip/2018/12/dataset.txt'

# from https://stackoverflow.com/a/21014653
def random_ip():
        return socket.inet_ntoa(struct.pack('>I', random.randint(1, 0xffffffff)))

def create_user():
        return json.dumps({
                'id': str(uuid4()),
                'ip': random_ip()
        })

with open(FILENAME, 'w') as f:
        for i in range(0, TOTAL_RECORDS):
                user = create_user()
                f.write(user + "\n")

Ok, now to finally run the test for our first hashing function. For that we need to read the data and calculate histogram. I decided to use 10000 buckets to give us more granularity on the hashed data. A common scenario could also be use 100 buckets (that could easily be mapped later to a percentage).

MAX_DOUBLE = float(0xFFFFFFFFFFFFFFFF)
BUCKETS = 10000
sums_md5 = [0] * BUCKETS

def md5_hash(uuid):
        return struct.unpack_from('Q', md5.new(uuid).digest())[0]

with open(FILENAME, 'r') as f:
        for line in f:
                data = line.rstrip()
                val = md5_hash(data)
                bucket = int((val / MAX_DOUBLE) * BUCKETS)
                sums_md5[bucket] += 1

The gist of it is that we calculate the md5 digest of every line in the file (a json dump of our user data), then we get the first 128 bit unsigned integer from that large number. After that, we normalize it to 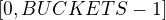and add a 1 to the bucket in sums_md5.

Now that we have the sums, we can calculate the Chi Squared test. The expected distribution is easy to get: we are expecting a uniform distribution, that is, the same number of elements in each bucket. How many? TOTAL_RECORDS / BUCKETS.

expected_q = float(TOTAL_RECORDS) / BUCKETS
expected = [expected_q] * BUCKETS

res = stats.chisquare(sums_md5, expected)
print(res)

Power_divergenceResult(statistic=10110.476, pvalue=0.21473669149106034)

Ok, we got a number. For our data set, MD5 results in 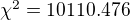. The probability to get that number is 21.47%. Since this is bigger than our threshold of 5%, we do not reject our null hypothesis and can say that MD5 is uniform (for our data set).

It's the time now for MurmurHash3. We'll do the same process: first, calculate histogram for the same dataset.

sums_murmur = [0] * BUCKETS

def murmur_hash(uuid):
                return mmh3.hash64(uuid, signed=False)[0]

with open(FILENAME, 'r') as f:
        for line in f:
                data = line.rstrip()
                val = murmur_hash(data)
                bucket = int((val / MAX_DOUBLE) * BUCKETS)
                sums_murmur[bucket] += 1

Now we can calculate the Chi Squared test for our observed data.

res = stats.chisquare(sums_murmur, expected)
print(res)

Power_divergenceResult(statistic=10084.668000000001, pvalue=0.27133381341907714)

We got very similar results than for MD5: 27% of getting that statistic. We can say MurmurHash3 is also uniform for our data set.

Finally, the same process but now for SpookyHash.

sums_spooky = [0] * BUCKETS

def spooky_hash_(uuid):
                return struct.unpack_from('Q', spooky_hash.Hash64(uuid).digest())[0]

with open(FILENAME, 'r') as f:
        for line in f:
                data = line.rstrip()
                val = spooky_hash_(data)
                bucket = int((val / MAX_DOUBLE) * BUCKETS)
                sums_spooky[bucket] += 1

And the Chi Squared test for the observed data.

res = stats.chisquare(sums_spooky, expected)
print(res)

Power_divergenceResult(statistic=10092.240000000002, pvalue=0.2539818853860341)

Again, this also seems to be uniform with a p-value of 25%.